はじめまして。Kondo Takayaです。こちらの記事では統計検定準1級へ合格するためにおこなった私の勉強法を紹介いたします。
初めての記事執筆ということもあり、読みづらいところもあるかもしれませんが、お読みいただき、合格に向け少しでもお役に立てると嬉しいです。
自己紹介
- B2Bマーケティング×データサイエンティストになるため、データサイエンスの勉強に日々取り組んでいます。
- 本業のB2Bマーケティングでは施策の企画立案から実行、インサイドセールス統括、営業へのトスアップ等のリードマネジメント業務を担当しています。ABMによる施策展開もおこなっています。
- 3年間(2020年~2022年)の資格取得履歴です。以下記載以外に基本情報技術者、ネットワークスペシャリストの資格も保持しています。統計検定の勉強は2020年頃から始めました。 ー2020年11月 統計検定2級 受験(合格:62点) ー2021年10月 CBAS:データ分析スキル実務検定 受験(合格)
合格までに勉強したこと
(1)時系列
2022年2月 統計検定準1級の勉強開始 2022年2月~2022年7月 勉強時間 約320時間 2022年7月 統計検定準1級受験【1回目】(39点 不合格) 2022年7月~2022年11月 勉強時間 約140時間 2022年11月 統計検定準1級受験【2回目】(80点 合格)
(2)書籍単位
<合計> 459時間
統計学実践ワークブック 198時間
統計検定準1級公式問題集(過去問) 112時間
明解演習数理統計 41時間
デ-タ解析のための統計モデリング入門 17時間
多変量解析法入門 13時間
入門統計学第2版 12時間
スバラシク実力がつくと評判の微分積分 11時間
スバラシク実力がつくと評判の確率統計 10時間
基礎からのベイズ統計学 8時間
多変量解析入門 線形から非線形へ 8時間
スバラシク実力がつくと評判の線形代数 6時間
完全独習ベイズ統計学入門 4時間
図解で分かる多変量解析 3時間
時系列解析 3時間
基礎からわかる時系列分析 3時間
経済・ファイナンスデ-タの計量時系列分析 3時間
Youtube 5時間
不合格になった勉強法
1回目の受験では、いろんな方の合格体験記を拝見して合格目安と想定した約300時間の勉強後、ギリギリ合格できるのでは?と思い受験したのですが、39点で不合格となりました。 振り返ってみると、不合格となった理由はとても明確です。 それは、統計学実践ワークブックの例題、過去問を過学習しすぎたことです。


受験1回目ではワークブックの例題、過去問を解けるようになれば6割取れるのでは?という考えで勉強していたのですが、考えがとても甘かったです。
受験して分かりましたが、過去問に掲載されている問題形式とは少し傾向が異なる気がしました。準1級に相当する知識を基本から理解していないと解けない問題が多かったな、という印象です。実践ワークブック、過去問題の過学習で解けると思ったのは多くても2割程度という印象です。
そのため、受験2回目に向けて基本から理解できるよう苦手な分野を勉強しなおすように勉強方針を改めました。
合格した勉強法
1回目の受験で失敗した過学習を避けるため、弱い分野を洗い出し、一から勉強し始めました。●月までにとにかく合格ほしい、ということではなく、統計学を基本的に理解したいという思いが強かったため、あまりスケジュールを意識せず取り組みました。
試験レポートにも記載されていますが、自分が点数を取れなかった弱点分野の3分野に特化した勉強を行い、2回目の受験で80点を獲得し、合格することができました。
ここからは1回目の受験から弱点分野を特定し、各分野に対して具体的にどのような勉強をしてきたのかを紹介します。
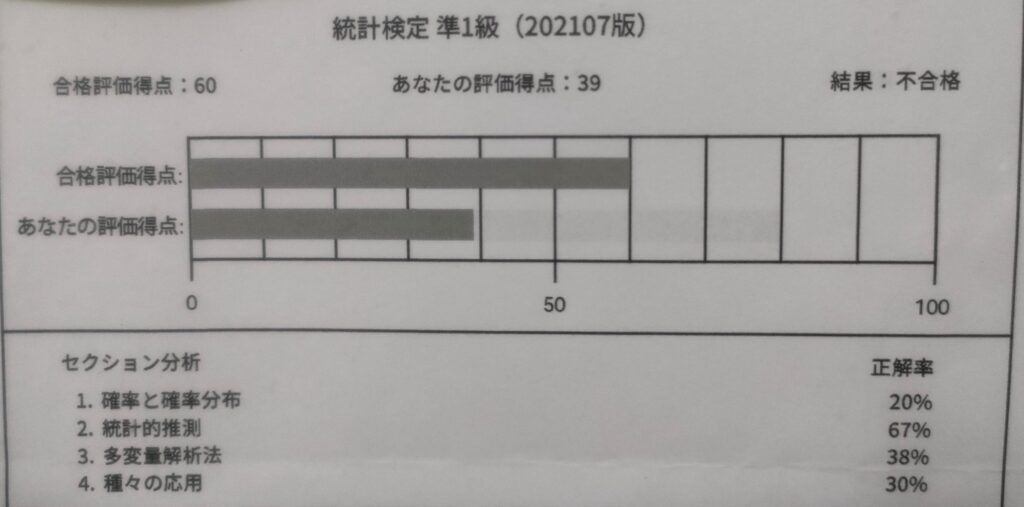
■受験結果から読み取れる弱点分野(セクション) ①確率と確率分布 ②多変量解析法 ③種々の応用
上の画像から「2.統計的観測」以外の分野(セクション)で60%以上の点数を獲得することができれば、合格できると考えました。
弱点①確率と確率分布
大変恥ずかしい話ですが受験1回目は統計学実践ワークブックを読んでいる時も微分積分で止まることが多く、googleで調べながら読み進めていました。こういう理解度だったこともあり、不合格になったのだと思います・・・。
微分積分が分からないと統計学を基本から理解できないと思い、微分積分を基礎から理解できるようマセマシリーズで勉強しました。微分積分はいろんな本が出版されていますが、本屋で見比べて自分に一番合う本はマセマシリーズだと思い、微分積分、線形代数、確率統計すべてマセマシリーズで勉強しました。
それぞれページ数は250ページほどありますが、2週間(約10時間)ほどで一通り読み終わります。マセマシリーズでは、教科書タイプ(紹介している本)と別に演習タイプも出版されています。私は演習タイプは実施しませんでした。
マセマシリーズは本当に基本から丁寧にまとめられているため、理解しやすいです。しかし、確率統計は途中から分からなくなることもあり、少し苦労しました。
ただ、丁寧に説明された後に例題というような構成になっていますので、分からなくなれば前のページに戻り読み直すと分かるようになるので、学習が止まることがなかったので、嬉しかったです。統計学実践ワークブックでは各章で止まることが多かったので・・・



マセマシリーズで基本を勉強した後、「確率と確率分布」の分野でもう少し強化しようと、「明解演習 数理統計」で勉強しました。本のタイトル通り、演習問題が中心で108問あります。
ただし、個人的にはマセマシリーズで理解した内容だけでは、全くスラスラ演習問題を解けず、何回もつまづき、そのたびにGoogleで調べて読み進めてきました。
正直合格した時点でもすべての演習問題をスラスラ解けるレベルには至っていませんでしたので、全問スラスラ解けるレベルにならなくても合格レベルには到達すると思います。個人的には、難易度の高い本だったなと思っています。

弱点②多変量解析法
この分野は1回目受験時に「図解でわかる多変量解析」を読んでいたのですが、まだまだ理解が浅かったようです。

新たに2冊購入し、再学習しました。オススメは「多変量解析法入門」→「多変量解析入門」の順番で読み進めることです。「多変量解析法入門」は統計学実践ワークブックで詳細説明されていなかった数量化1類、数量化2類、数量化3類についてとても丁寧に説明されています。
この本を読んで初めて知ったことも多いです。
例えば、数量化1類は重回帰分析の質的変数ver、数量化2類は判別分析の質的変数ver、数量化3類は主成分分析の質的変数verということを知り、各分析との関連性を把握することで頭の中の整理もでき、多変量解析についてとても理解が深まりました。
統計学実践ワークブックでは多変量解析の章は簡潔に説明されていたため、なかなか本質を理解することができませんでした。しかし、こちらの本では各解析についても具体例を使って説明されており、とても分かりやすいのでオススメです。

「多変量解析入門」は「多変量解析法入門」で得た基礎知識を強化するため、読みました。数式を使った説明がメインであり、読み進めていくうえで分からないことも出てきますが、こちらの本も各章とても丁寧に説明されており、分かりやすいです。
個人的にはサポートベクターマシンについて私が読んだ本の中で一番詳しく書かれていた気がします。サポートベクターマシンについて詳しく読みたかったので、購入したというのも購入理由の1つです。

弱点③種々の応用
この分野は具体的にどこを勉強すればよかったか分からなかったため、統計学実践ワークブックを1章から読み直して、分からない言葉は徹底的に調べるということを行いました。
弱点対策後の再受験結果
最終的に上で紹介した勉強を行い、再受験したところ合格することができました。
なお、上で記載していた勉強以外にも統計学実践ワークブックの読み直し、過去問題の解きなおしも再受験前におこなっています。

合格後に気づいたオススメの勉強法
統計検定準1級に合格して気づいたオススメの勉強法です。あくまで個人の意見です。合格を保証するものではないため、その点ご注意下さい。
(1)はじめに①(微分・積分、線形代数)
統計学実践ワークブックでは知っていることが大前提で微分・積分、線形代数が使われており、微分・積分、線形代数の知識が浅いとかなり読み進めるのにかなり苦労します。 (私がそうでしたので・・・汗)
こちらの記事でも紹介しておりますが、マセマシリーズの微分・積分、線形代数の一読をオススメします。どちらも分かりやすく、簡単な内容ですので、2週間(約10時間)ほどあれば一読できます。


(2)はじめに②(入門統計学)
統計学実践ワークブックを本格的に読み始める前にオススメしたい本がもう1冊あります。並行で読むというのでもいいと思います。
私は統計検定2級合格後、約1年3ヶ月ほどの空白期間をおいて準1級の勉強をしましたが、期間が空いてしまったので統計学の内容を忘れていることもあり、ワークブックを1周するのにとても苦労しました。
こちらの「入門統計学第2版」は、統計学実践ワークブックで瀬悦明されている内容をある程度網羅されており、とても分かりやすく説明していますのでオススメです。
具体的な章立ては以下です。
第1章 記述統計学 第2章 確率分布 第3章 推測統計学 第4章 信頼区間の推定 第5章 カイ二乗分布とF分布 第6章 仮説検定と検出力 第7章 2群の平均の差の検定 第8章 分散分析 第9章 多重比較法 第10章 実験計画法 第11章 ノンパラメトリック検定 第12章~第14章 多変量解析 第15章 ベイズ統計学

なお、第2版と別に第1版もあります。第1版はノンパラメトリック検定が2章立てになっており、より詳細に説明されています。私は第1版含めて2冊購入しましたが、この第2版だけでも問題ないかなと思いました。
(3)統計学実践ワークブック、過去問題集
統計検定準1級の合格に向けて、この本の購入はmustだと思います。この本がなかった当時に合格された方は本当にいろんな本を読まれて、合格されたのだろうなと思いました。(尊敬します・・・)
中身を読んでも分からないこともたくさんあると思いますが、これだけ広い分野を簡潔にポイントを記載してまとめられているこの本はかなりの良書であると思います。 (統計検定準1級を合格する方をターゲットにした本としては)
この本は各章に例題(過去門と同等)が数問記載されています。各章を読んだだけでは理解が難しいと思いますので、こちらの例題と過去問をセットで解いて読み進めていくことが良いと思います。
何度も何度もこの本を読みましたが、章が進むたびに初めの章の内容を忘れてしまっていることが多く、とても苦労しました。
その後、章ごとに例題と過去問をセットで解くということを行い、知識が定着化されましたので、とてもオススメです。
こーしさんの統計検定準1級(CBT)の難易度を解説!【合格体験談】にはとてもお世話になりました。記事内に「統計検定準1級の出題傾向」という箇所があり、そちらに統計学実践ワークブックと過去問の章ごとの割り当てが紹介されています。 (こーしさん、本当に素敵な記事をありがとうございました!)

過去問は論述問題も収録されていますが、CBT試験で合格だけを目指すのであれば、飛ばしても大丈夫だと思います。

(4)受験前のオススメ①(確率統計)
統計学実践ワークブックだけでは確率統計を理解することは難しいです。マセマシリーズ「確率統計」、「明解演習 数理統計」で確率統計分野の強化をオススメします。
なお、どちらも難しい内容がごくたまに記載されています。すべてを完全に理解できなくても統計検定準1級の合格はできると思います。


(5)受験前のオススメ②(多変量解析)
受験レポートのセクション分析でも記載されていますが、こちらの分野の勉強は合格に向けて必須だと思います。記事内でも紹介していますが、以下2冊がオススメです。


(6)受験前のオススメ③(ベイズ統計学)
ベイズ統計学は統計学実践ワークブックでも紹介されていますが、本当に分かりづらいです。初学者はこの本だけで理解するはとても難しいのではないかと思います。
私は以下2冊でベイズ統計学を追加で勉強しました。統計検定2級の時にお世話になった「完全独習 統計学入門」を執筆されている小島さんの書籍で、ベイズ統計学もとても丁寧に分かりやすく説明されています。
ワークブックを一度読み終えて読む場合は、分かる内容も多々含まれているかと思いますので、ポイントだけ読み進めていくという読み方もありだと思います。
基本からベイズ統計学を丁寧に紹介されていますので、図書館などでの借りて読むというレベルでもいいかもしれません。(私はそうしました。図書館で読んでから、購入するというスタイルで読んでいたこともありまして)

また、上でご紹介した本に加えて統計検定準1級合格レベルのベイズ統計学を理解するために、この本の購読はとてもオススメです。
この本ではベイズの定理、ベイズ推定、メトロポリス・ヘイスティングス法、ハミルトニアンモンテカルロ法についてそれぞれ1章を使って丁寧に説明されており、とても分かりやすいです。
個人的に読みやすかったポイントは、各章の章末問題とは別に具体例を用いた問題があり、その問題を考えながら内容を勉強することでより理解を深めることができました。
例えば、ベイズの定理では3囚人問題と記載された具体例で説明されています。(定理など数式だけでは、中身を理解することができないタイプですので、こういった具体例にとても助けられました。)

(7)参考(オススメサイト・動画)
準1級の勉強をしていた当時Twitterでもよくつぶやいていましたが、本当に分からないことが多く、「先生がいるといいのにな・・」と何度も思いました。そんなとき、以下のWebサイト、Youtubeでとても助けられましたので、紹介いたします。
・あつまれ統計の森
過去問題の解説を見ても分からなかったとき、統計学実践ワークブックの例題の解説で分からなかったときなど、問題を解くときにとてもお世話になりました。細かく解説いただいており、大変助けられました。
統計検定準1級 解説 〜過去問解答例・解説 & 公式ワークブックの解答例・解説〜
・えびかずきさんのnote
統計学実践ワークブックの例題解説で分からなかったとき、「あつまれ統計の森」サイトと併用して活用させていただきました。こちらのサイトにも大変助けられました。
微分積分、線形代数をマセマシリーズで勉強する前によく視聴させていただいておりました。
初めて視聴させていただいたのはベイズ統計シリーズでした。書籍だけではどうしても理解できなかったとき、よく視聴させていただいておりました。アイシアさんに癒されながら、統計についても学ぶことができるとても素晴らしい動画ばかりです。
広島大学の大学院の発表だと思うのですが、マルコフモンテカルロ法について紹介されています。
最後に
初めての記事執筆ということもあり、とても読みづらいところもあったかと思いますが、最後までお読みいただきありがとうございます。貴重なお時間を私の記事に割いていただき、ありがとうございます。
お読みいただけました方へ少しでもお役に立てればとても嬉しい限りです。
合格を祈念しております!


コメント